算法设计与分析基础笔记

递归算法数序分析

在计算一些常用算法的时间复杂度时，经常涉及到递归，因此也就离不开递归算法的分析

先看一个例子

计算函数的时间复杂度

void fun(int n){
    if(n<=0){
        return 1;
    }else{
        return n*f(n-1);
    }
}

上面函数的基本操作就是做乘法，所以计算函数的时间复杂度，其实就是计算乘法的操作次数。

假设M(n)代表传入参数n时，函数进行乘法操作的次数，所以有

$$M(n)= \begin{cases} 0\quad\textcolor{orange}{n=0}; \\ M(n-1)+1\quad\textcolor{orange}{n>0};\\ \end{cases}$$

其中加1是指将n乘以f(n-1)。所以根据上面的公式得

$$\begin{aligned} M(n)&=M(n-1)+1\\ &=M(n-2)+1+1\\ &=M(n-3)+1+1+1\\ &=M(n-4)+1+1+1+1\\ &=···\\ &=M(0)+n\\ &=n \\ \end{aligned}$$

$\begin{aligned}
时间复杂度 \textcolor{red}{O(n)=n}
\end{aligned} $

进行递归算法分析的主要步骤

• 确定输入参数的规模
• 找出基本操作
• 分析相同规模不同输入的算法的最优、最差、平均效率差别
• 建立递推关系
• 解递推式

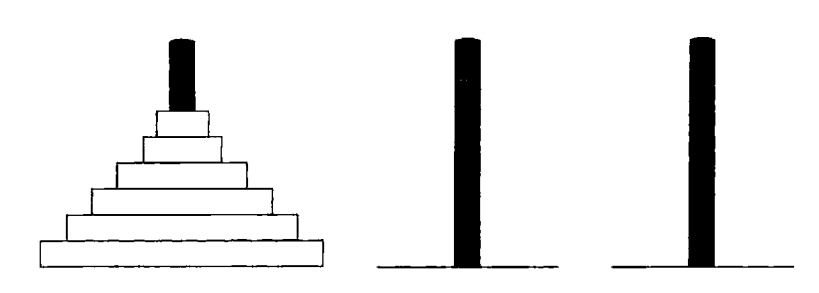
汉诺塔递归算法分析

汉诺塔游戏是将n个盘子通过一个中间柱子，移动到第三个柱子，规则就是小盘子必须在大盘子上面。

问题可以分解成三步，先将上面的n-1个盘子移动到第二根柱子，然后把最大的盘子移动到第三根柱子，最后把n-1个盘子移动到第三根柱子。假设$M(n)$表示将n个盘子移动到第三根柱子需要的步骤数，所以有以下递推式

$$\begin{aligned} &M(n)=M(n-1)+1+M(n-1) \\ &M(n)=2M(n-1)+1\\\\ &M(n)= \begin{cases} 1\quad\textcolor{orange}{n=1}; \\\\ 2M(n-1)+1\quad\textcolor{orange}{n>0};\\ \end{cases} \end{aligned}$$

所以有

$$\begin{aligned} \textcolor{green}{ M(n) } &=2M(n-1)+1\\ &=2^2M(n-2)+1+2^1\\ &=2^3M(n-3)+1+2^1+2^2\\ &=2^4M(n-4)+1+2^1+2^2+2^3\\ &=···\\ &=2^{n-1}M(1)+1+2+2^2+2^3+···2^{n-2}\\ &=2^{n-1}+\frac{1-2^{n-1}}{1-2}\\ &=2^{n-1}+2^{n-1}-1\\ &=\textcolor{red}{2^n-1}\\\\ 时间复杂度：\textcolor{red}{O(n)=2^n} \end{aligned}$$

再看一个例子

计算时间复杂度

void fun(int n){
    if(n==1){
        return 1;
    }else{
        return f(n/2)+1;
    }
}

这种类型的不能用反向替换方法，如果像 $M(n)=M(\frac{n}{2})+1 \\\space\space M(\frac{n}{2})=M(\frac{n}{4})+1$ 这样替换下去，n不是2的乘方的话，终止不了的。只能在n为2的k次方的情况下求解递推式，所以假设 $n=2^k$

上公式

$$\begin{aligned} &令 n=2^k \\ {\space\space} &M(n)=M(\frac{n}{2})+1 \\&=>M(2^k)=M(2^{k-1})+1 \\&M(1)=0\\ \end{aligned} \begin{aligned} M(2^k) &=M(2^{k-1})+1 \\ &=M(2^{k-2})+1+1\\ &=M(2^{k-3})+1+1+1\\ &=···\\ &=M(2^{k-k})+1+1+···+1+1+1\\ &=M(1)+k\\ &=\textcolor{red}{k}\\2^k=n {\space\space}即{\space\space}k=log_2n{\space\space} 所以M(n)=log_2n\\ 时间复杂度：\textcolor{red}{O(n)=log_2n} \end{aligned}$$

其他的$\frac{n}{3},\frac{n}{4}$都是一样的道理